El equilibrio redox debe su nombre a las semirreacciones simultáneas de oxidación y reducción, guarda bastantes similitudes con el resto de equilibrios químicos: si en el equilibrio ácido/base se intercambiaban protones, y en el equilibrio de complejación se intercambiaban ligandos, en el equilibrio redox se van a intercambiar electrones.
Complemento: potenciales normales de reducción
Consulta este apéndice.
Ejercicios
"El fluoruro de plata reacciona con hierro sólido para formar el fluoruro ferroso y plata neutra, escribe la reacción química ajustada e identifica las especies que se oxidan y se reducen"
La reacción química ajustada es la siguiente: 2AgF(aq) + Fe(s) <====> FeF2(aq) + 2Ag(s)
escribimos debajo los distintos números de oxidación de cada átomo: +1 -1 0 +2 -1 0
observando esos números de oxidación concluimos lo siguiente:
Ag pasa de estado +1 a estado 0: la plata se ha reducido.
Fe pasa de estado 0 a estado +2: el hierro se ha oxidado.
F se mantiene con estado -1 a ambos lados de la reacción, no sufre porceso redox alguno.
Puesto que AgF provoca la oxidación de Fe, podemos decir igualmente que AgF es el agente oxidante. Y puesto que Fe produce la reducción de Ag, podemos decir que Fe es el agente reductor.
Evidentemente, en el lado derecho de la reacción química se han formado los correspondientes pares redox conjugados: el catión Fe2+ es el conjugado de Fe, mientras que Ag es el conjugado de Ag+.
"Para las siguientes pilas, identificar cuál es el ánodo y el cátodo, el proceso redox que tiene lugar, y el correspondiente potencial estándar."
Para resolver este ejercicio es necesario consultar los potenciales estándar de reducción que se adjuntan en el correspondiente apéndice.
a) Zn|Zn2+||Pb2+|Pb
Zn se oxida: ÁNODO Zn - 2e- <==> Zn2+ E0 = 0,7626V (signo cambiado por tratarse de una oxidación)
Pb se reduce: CÁTODO Pb2+ + 2e- <==> Pb E0 = -0,126V
Proceso redox global: Zn + Pb2+ <==> Zn2+ + Pb E0 = 0,6366V
b) Ni|Ni2+||Ag+|Ag
Ni se oxida: ÁNODO Ni - 2e- <==> Ni2+ E0 = 0,257V (signo cambiado por tratarse de una oxidación)
Ag se reduce: CÁTODO Ag+ + 1e- <==> Ag (x2) E0 = 0,7991V
Proceso redox global: Ni + 2Ag+ <==> Ni2+ + 2Ag E0 = 1,0561V
"Calcular los potenciales de las pilas anteriores si las concentraciones iónicas son de 0,1M y de 0,01M."
Los valores de potencial calculados en el problema anterior corresponden a potenciales estándar, donde se considera que las concentraciones iónicas son todas ellas de 1M. Para calcular los potenciales de esas pilas a diferentes concentraciones es necesario utilizar la ecuación de Nernst:
donde Q es el cociente de reacción del proceso redox global y que solo tiene en cuenta las especies iónicas, mientras que z es el número de electrones intercambiados entre el ánodo y el cátodo.
a) Zn|Zn2+||Pb2+|Pb
Proceso redox global: Zn + Pb2+ <==> Zn2+ + Pb E0 = 0,6366V
La reacción química ajustada es la siguiente: 2AgF(aq) + Fe(s) <====> FeF2(aq) + 2Ag(s)
escribimos debajo los distintos números de oxidación de cada átomo: +1 -1 0 +2 -1 0
observando esos números de oxidación concluimos lo siguiente:
Ag pasa de estado +1 a estado 0: la plata se ha reducido.
Fe pasa de estado 0 a estado +2: el hierro se ha oxidado.
F se mantiene con estado -1 a ambos lados de la reacción, no sufre porceso redox alguno.
Puesto que AgF provoca la oxidación de Fe, podemos decir igualmente que AgF es el agente oxidante. Y puesto que Fe produce la reducción de Ag, podemos decir que Fe es el agente reductor.
Evidentemente, en el lado derecho de la reacción química se han formado los correspondientes pares redox conjugados: el catión Fe2+ es el conjugado de Fe, mientras que Ag es el conjugado de Ag+.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Para las siguientes pilas, identificar cuál es el ánodo y el cátodo, el proceso redox que tiene lugar, y el correspondiente potencial estándar."
Para resolver este ejercicio es necesario consultar los potenciales estándar de reducción que se adjuntan en el correspondiente apéndice.
a) Zn|Zn2+||Pb2+|Pb
Zn se oxida: ÁNODO Zn - 2e- <==> Zn2+ E0 = 0,7626V (signo cambiado por tratarse de una oxidación)
Pb se reduce: CÁTODO Pb2+ + 2e- <==> Pb E0 = -0,126V
Proceso redox global: Zn + Pb2+ <==> Zn2+ + Pb E0 = 0,6366V
b) Ni|Ni2+||Ag+|Ag
Ni se oxida: ÁNODO Ni - 2e- <==> Ni2+ E0 = 0,257V (signo cambiado por tratarse de una oxidación)
Ag se reduce: CÁTODO Ag+ + 1e- <==> Ag (x2) E0 = 0,7991V
Proceso redox global: Ni + 2Ag+ <==> Ni2+ + 2Ag E0 = 1,0561V
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Calcular los potenciales de las pilas anteriores si las concentraciones iónicas son de 0,1M y de 0,01M."
Los valores de potencial calculados en el problema anterior corresponden a potenciales estándar, donde se considera que las concentraciones iónicas son todas ellas de 1M. Para calcular los potenciales de esas pilas a diferentes concentraciones es necesario utilizar la ecuación de Nernst:
a) Zn|Zn2+||Pb2+|Pb
Proceso redox global: Zn + Pb2+ <==> Zn2+ + Pb E0 = 0,6366V
en este caso da igual que cambiemos los valores de las concentraciones iónicas, si ambas son iguales a 1M, 0,1M ó 0,01M, el cociente Q = 1, por loque logQ = 0 y...
E = E0 = 0,6366V
b) Ni|Ni2+||Ag+|Ag
Proceso redox global: Ni + 2Ag+ <==> Ni2+ + 2Ag E0 = 1,0561V
nótese que ahora dada la estequiometría del proceso redox global, la expresión de Q es algo diferente porque [Ag+] está elevada a 2, por tanto ahora Q no va a ser 1 como ocurría en el apartado anterior. Si tomamos concentraciones iónicas de 0,1 y 0,01M los resultados que se obtienen son los siguientes:
E = 1,0266V para conc. de 0,1M ; E = 0,9971V para conc. de 0,01M
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Calcular la constante de equilibrio químico para cada una de las dos pilas anteriores."
Seguimos utilizando la ecuación de Nernst, pero ahora igualaremos esa ecuación a 0 para conseguir su estado de equilibrio químico, operando la ecuación de Nernst igualada a 0 obtenemos la expresión de la constante de equilibrio químico del proceso redox global de la siguiente manera:
en ambas pilas sustituiremos el número de electrones intercambiados, que es 2 en ambos casos, y los valores de E0 calculados en el segundo problema de esta entrada, obteniendo así los siguientes valores:
a) Zn|Zn2+||Pb2+|Pb K = 1021,58 ; b) Ni|Ni2+||Ag+|Ag K = 1035,8
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Calcular el potencial del sistema Fe2+/Fe3+ si la concentración de ambos cationes es de 0,01M en presencia de una disolución de o-fenantrolina (1M), sabiendo que las constantes de formación de los complejos Fe(ph)32+ y Fe(ph)33+ son 1017,2 y 107,2 respectivamente."
El proceso redox propuesto es el siguiente: Fe2+ - 1e- <==> Fe3+ y su E0 = -0,771V
para conocer el potencial real debemos utilizar de nuevo la ecuación de Nernst:
por tanto, debemos calcular las concentraciones libres de Fe2+ y Fe3+ que hay en esa disolución que contiene un agente complejante como es la o-fenantrolina. Para el Fe2+:
fin ? aprox 1 0,01
nos valemos de la constante de formación del complejo para despejar [Fe2+] libre:
Repetimos el mismo proceso para Fe3+:
fin ? aprox 1 0,01
nos valemos de la constante de formación del complejo para despejar [Fe3+] libre:
Una vez hemos calculado las concentraciones libres de ambos cationes del hierro, podemos sustituir en la ecuación de Nernst para calcular elpotencial real de la disolución:
en estos problemas es muy importante indicar si el potencial obtenido corresponde a la oxidación o a la reducción del sistema, recordad que el potencial de una oxidación es igual al potencial de la reducción pero con signo contrario.
"Calcular el potencial del sistema Ag+/Ag en un medio de KCl 1M."
El sistema propuesto es una reducción: Ag+ + 1e- <==> Ag y según la tabla su E0 = 0,7991V
la expresión de la ecuación de Nernst para este sistema es la siguiente:
por tanto, ahora solo tenemos que calcular la concentración de [Ag+] libre en un medio de KCl 1M, sabiendo que Ag+ formará el correspondiente precipitado de AgCl, cuya constante de solubilidad según la tabla es de pKs = 9,75, usaremos la expresión matemática de Ks para determinar [Ag+] libre:
sustituimos ese valor en la ecuación de Nernst y obtenemos el potencial real del sistema:
"A una disolución 0,5M de nitrato de plata se le añade cadmio sólido en exceso. Calcular la concentración de iones plata una vez se ha alcanzado el equilibrio."
AgNO3 es una sal totalmente soluble, por lo que en la disolución tendremos 0,5M de cationes Ag+. Puesto que se añade Cd neutro en exceso, cabe esperar que todos los cationes Ag+ se reduzcan a Ag a costa de oxidar parte del Cd a Cd2+. Planteamos ambas semirreacciones:
reducción: Ag+ + 1e- <==> Ag (x2) E0 = 0,7991V
oxidación: Cd + 2e- <==> Cd2+ E0 = 0,403V
redox: 2Ag+ + Cd <==> 2Ag + Cd2+ E0 = 1,2021V
tratamos ahora el problema como si fuera de equilibrio químico, planteando en la ecuación obtenida una situación inicial y otra final:
fin: ? exc - 0,5/2
puesto que hay Cd en exceso y el proceso redox es espontáneo (E0>0) consideramos que prácticamente todos los iones Ag+ reaccionan para dar lugar a la mitad de iones Cd2+, dada la estequiometría de la reacción. Para esta reacción química tendremos su correspondiente constante de equilibrio:
pero de este tema hemos aprendido a calcular la constante de equilibrio de un proceso redox en función de su E0:
sustituyendo el valor de K en la primera ecuación, ya podemos calcular [Ag+] libre en la disolución:
El proceso redox propuesto es el siguiente: Fe2+ - 1e- <==> Fe3+ y su E0 = -0,771V
para conocer el potencial real debemos utilizar de nuevo la ecuación de Nernst:
Fe2+ + 3ph <==> Fe(ph)32+
inicio 0,01 1 -fin ? aprox 1 0,01
nos valemos de la constante de formación del complejo para despejar [Fe2+] libre:
Fe3+ + 3ph <==> Fe(ph)33+
inicio 0,01 1 -fin ? aprox 1 0,01
nos valemos de la constante de formación del complejo para despejar [Fe3+] libre:
Solución: -1,361V para la oxidación de Fe2+ a Fe3+ en condiciones especiales
en estos problemas es muy importante indicar si el potencial obtenido corresponde a la oxidación o a la reducción del sistema, recordad que el potencial de una oxidación es igual al potencial de la reducción pero con signo contrario.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Calcular el potencial del sistema Ag+/Ag en un medio de KCl 1M."
El sistema propuesto es una reducción: Ag+ + 1e- <==> Ag y según la tabla su E0 = 0,7991V
la expresión de la ecuación de Nernst para este sistema es la siguiente:
Solución: 0,224V para la reducción de Ag+ a Ag en condiciones especiales
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"A una disolución 0,5M de nitrato de plata se le añade cadmio sólido en exceso. Calcular la concentración de iones plata una vez se ha alcanzado el equilibrio."
AgNO3 es una sal totalmente soluble, por lo que en la disolución tendremos 0,5M de cationes Ag+. Puesto que se añade Cd neutro en exceso, cabe esperar que todos los cationes Ag+ se reduzcan a Ag a costa de oxidar parte del Cd a Cd2+. Planteamos ambas semirreacciones:
reducción: Ag+ + 1e- <==> Ag (x2) E0 = 0,7991V
oxidación: Cd + 2e- <==> Cd2+ E0 = 0,403V
redox: 2Ag+ + Cd <==> 2Ag + Cd2+ E0 = 1,2021V
tratamos ahora el problema como si fuera de equilibrio químico, planteando en la ecuación obtenida una situación inicial y otra final:
2Ag+ + Cd <==> 2Ag + Cd2+
inicio: 0,5 exc - -fin: ? exc - 0,5/2
puesto que hay Cd en exceso y el proceso redox es espontáneo (E0>0) consideramos que prácticamente todos los iones Ag+ reaccionan para dar lugar a la mitad de iones Cd2+, dada la estequiometría de la reacción. Para esta reacción química tendremos su correspondiente constante de equilibrio:
Solución: [Ag+] libre = 2,11·10-21 M
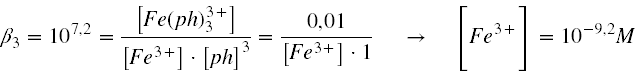
No hay comentarios:
Publicar un comentario