En el tema anterior de Termodinámica, estudiamos los aspectos energéticos de las reacciones químicas y bajo qué condiciones esas reacciones eran favorables de transcurrir, sin embargo, no comentamos nada del tiempo que tardan esas reacciones en producirse. De ello vamos a tratar en este tema: la Cinética Química.
Ejercicios
"Para la descomposición del pentacloruro de fósforo en cloro diatómico y tricloruro de fósforo, se han obtenido los siguientes resultados:
[PCl5] [M] 0,466 0,400 0,360 0,330 0,310
t (s) 0 90 150 270 420
Calcular la velocidad media para cada intervalo de tiempo."
Escribimos en primer lugar la reacción química:
puesto que nos dan datos de concentración del único reactivo de nuestra reacción, realizaremos nuestro estudio cinético con ese reactivo PCl5:
de esta forma, podemos sustituir los incrementos de tiempo y los decrementos de concentración para obtener una serie de velocidades medias, por ejemplo, el primer caso será:
usaríamos la misma ecuación para calcular las velocidades medias para todos los intervalos de tiempo, de tal manera que esas velocidades medias serían las siguientes:
SOLUCIÓN:
nótese que a medida que transcurre la reacción, la concentración de reactivo va disminuyendo, por tanto, la velocidad de reacción también disminuye conforme se agota el reactivo.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"En la oxidación del amoníaco:
se sabe que la velocidad inicial de formación de nitrógeno es de 0,05mol/Ls. Calcular las velocidades de desaparición del amoníaco y del oxígeno."
La expresión matemática del único dato numérico que nos dan es la siguiente:
por otra parte, sabemos que para esta reacción concreta, la velocidad general es la siguiente:
por tanto, ya podemos despejar y calcular las velocidades iniciales de desaparición de ambos reactivos: SOLUCIONES:
nótese que puesto que hemos calculado velocidades de desaparición de reactivos, éstas tendrán valores negativos.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
"Para la reacción química
se obtienen los siguientes datos de un estudio cinético:
determinar el orden de reacción y la constante de velocidad."
Fijándonos en las dos primeras experiencias descritas en la tabla, vemos que en ambas se mantiene constante [CO] pero se varía [NO2], vemos entonces que al duplicar [NO2] se duplica también la velocidad de reacción, es decir, que [NO2] y la velocidad varían en una relación lineal y no exponencial, por lo que el orden de reacción respecto al NO2 es 1.
Algo muy similar ocurre con la experiencia 3, pero en este caso se ha mantenido constante [NO2] y se ha duplicado [CO], observándose igualmente que la velocidad de reacción también se duplica, por tanto, esta reacción también es de orden 1 respecto al CO.
SOLUCIÓN: La reacción es de orden 1 para ambos reactivos, por lo que su orden global será 1+1=2
por tanto, la expresión de la velocidad de esta reacción será la siguiente:
de ella podemos despejar la constante de velocidad k:
y ya podemos sustituir los valores de cualquiera de las tres experiencias tabuladas en el enunciado.
SOLUCIÓN: k = 1,9 L/mol·s
observar las unidades de k para una reacción de orden global 2.
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Complemento: ecuación integrada de velocidad
Existe una forma adicional de escribir la ecuación de velocidad de una reacción química conociendo de antemano los órdenes parciales de cada reactivo que interviene en esa reacción, ello se consigue integrando la expresión general de la ecuación de velocidad. Así, tomando una reacción química general:
nos fijamos únicamente en el reactivo A, poniendo una concentración excesiva de B para que éste permanezca aproximadamente constante, de tal manera que para el reactivo A, la ecuación de velocidad será:
recordemos que es una velocidad de desaparición de reactivo, por tanto su signo será negativo. En función de cuál sea el orden de reacción respecto al reactivo A, esa velocidad tendrá varias expresiones:
si ahora operamos e integramos esas tres ecuaciones:
observamos que nos quedan una serie de ecuaciones que se pueden representar gráficamente:
en función de cómo representemos [A] frente a t, obtendremos diferentes gráficas que se volverán rectas cuando averigüemos el orden de reacción, además las pendientes y ordenadas en origen nos revelarán los valores de la constante de velocidad k y [A]0 respectivamente.






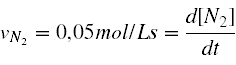














No hay comentarios:
Publicar un comentario